Pengertian dan Jenis Getaran Mekanik
Pengertian Getaran
Getaran merupakan suatu gerak bolak-balik pada interval waktu tertentu. Getaran memiliki hubungan dengan gerak osilasi dari benda serta gaya-gaya yang berhubungan dengan gerak benda tersebut. Setiap benda bermassa serta memiliki nilai elastisitas akan mengalami getaran saat diterapkan suatu gaya, misalnya dalam kasus konstruksi dari mesin dan struktur rekayasa seringkali mengalami fenomena getaran hingga mencapai derajat tertentu dan perlunya rancangan yang mempertimbnagkan sifat osilasi dari benda tersebut.
Getaran mempunyai nilai amplitudo, yaitu jarak pada simpangan yang terjauh dari titik kesetimbangan. Kesetimbangan merupakan suatu keadaan dimana benda berada pada posisi diam jika tidak ada gaya yang bekerja pada benda tersebut.
Jenis Getaran
Terdapat dua jenis getaran yaitu, getaran bebas dan getaran paksa. Getaran bebas terjadi apabila sistem mekanis diberi suatu gaya awal kemudian dibiarkan bergetar dengan bebas, sedangkan pada getaran paksa dapat terjadi apabila gerakan atau gaya bolak-balik diberikan pada sistem mekanis tersebut.
A. Getaran Bebas
Getaran bebas terjadi jika suatu sistem berosilasi karena terdapat gaya yang bekerja dalam sistem itu sendiri ataupun jika terdapat gaya luas yang bekerja pada sistem tersebut. Suatu sistem yang bergetar bebas akan bergerak pada satu atau lebih frekuensi natural dan merupakan sifat pada sistem dinamika yang terbentuk oleh distribusi kekuatan dan massanya. Suatu sistem yang mempunyai massa dan sifat elastisitas akan mengalami getaran bebas apabila diberikan gaya awal pada sistem tersebut. Contoh aplikasi dari getaran bebas yaitu sebuah bandul yang ditarik kemudian dilepas sehingga bandul tersebut melakukan getaran bebas dengan sendirinya.
Getaran bebas dapat diklasifikasikan menjadi dua jenis yaitu getaran bebas tanpa peredam dan getaran bebas dengan peredam.
1. Getaran Bebas Tanpa Peredam
Pada model sistem yang sederhana redaman dianggap bisa diabaikan, dan tidak terdapat gaya luar yang mempengaruhi massa sistem tersebut (getaran bebas).
 |
| Getaran Bebas Tanpa Peredam |
Dalam keadaan ini gaya yang bekerja pada pegas (Fs) akan sebanding dengan peregangan dari x, sesuai dengan teori hukum Hooke dan dirumuskan secara matematis sebagai berikut :
Berdasarkan Hukum Newton II, maka gaya yang dihasilkan sebanding dengan percepatan massa:
Karena F = Fs, maka diperoleh persamaan diferensial biasa sebagai berikut :
Apabila getaran sistem dilakukan dengan meregangkan pegas sejauh A kemudian dilepaskan, maka solusi dari persamaan di atas dan memberikan gerakan massa yaitu :
Solusi tersebut menyatakan bahwa massa dapat berosilasi dalam gerak harmonis sederhana (GHS) yang memiliki nilai amplitudo (A) dan frekuensi (fn). Bilangan fn merupakan frekuensi alami tak redam, yaitu suatu besaran yang penting dalam menganalisa fenomena getaran. Pada sistem massa pegas sederhana, frekuensi alami tak redam (fn) didefinisikan sebagai berikut:
2. Getaran Bebas Dengan Redaman
Apabila redaman diperhitungkan, berarti gaya redaman pada sistem juga berlaku pada massa selain gaya oleh peregangan pegas. Jika suatu benda bergerak dalam fluida, maka benda tersebut akan mendapatkan redaman karena kekentalan dari fluida.
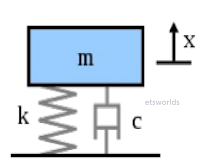 |
| Getaran Bebas Dengan Redaman |
Gaya dari kekentalan ini akan sebanding dengan kecepatan benda. Konstanta akibat kekentalan fluida (viskositas) dinamakan dengan koefisien peredam dengan satuan N.s/m.
Dengan menjumlahkan gaya yang bekerja pada benda maka diperoleh persamaan sebagai berikut.
Solusi dari persamaan ini bergantung pada besarnya nilain peredaman. Apabila redaman kecil, maka sistem masih dapat bergetar namun kemudian lambat laun akan berhenti, atau biasa disebut dengan istilah (kurang redam) dan merupakan kasus yang umumnya memerlukan perhatian dalam analisa getaran. Jika redaman diperbesar sehingga sistem tidak dapat lagi berosilasi maka titik tersebut dikenal dengan titik redaman kritis. Jika redaman terus ditambahkan hingga melewati titik kritis, maka sistem tersebut dalam keadaan lewat redam. Nilai koefisien peredaman yang dibutuhkan hingga mencapai titik redam kritis pada suatu model massa-pegas-peredam adalah sebagai berikut :
Untuk mengkarakterisasi jumlah dari redaman dalam suatu sistem digunakan nisbah redaman. Nisbah redaman adalah perbandingan antara redaman sebenarnya dengan jumlah redaman yang dibutuhkan agar diperoleh titik redaman kritis. Rumus untuk nisbah redaman adalah sebagai berikut.
Sebagai contoh, suatu struktur logam mempunyai nisbah redaman yang lebih kecil dari 0,05, sedangkan suspensi otomotif berada di selang 0,2 sampai 0,3. Solusi untuk sistem kurang redam pada suatu model massa-pegasperedam adalah sebagai berikut.
Nilai X, ingsutan fase dan amplitudo awal ditentukan berdasarkan panjang regangan pegas. Menurut solusi tersebut perlu diperhatikan dua hal yaitu: fungsi cosinus dan faktor eksponensial. Fungsi kosinus mewakili osilasi dari sistem, namun frekuensi osilasi akan berbeda daripada kasus yang tidak teredam. Sedangkan faktor eksponensial menentukan seberapa cepat sistem mengalami redaman: jika semakin besar nisbah redaman, maka akan semakin cepat sistem teredam hingga ke titik nol. Frekuensi dalam hal ini biasa disebut frekuensi alamiah teredam (fd) dan terhubung dengan frekuensi alamiah tanpa redam dengan persamaan berikut.
Frekuensi alamiah redam lebih kecil daripada frekuensi alamiah tak redam, akan tetapi untuk beberapa kasus praktis pada nisbah redaman relatif kecil, dan oleh karena itu perbedaan tersebut dapat diabaikan. Deskripsi dari teredam dan tak teredam kerap kali tidak disebutkan ketika menyebutkan frekuensi alamiah.
B. Getaran Paksa
| Getaran Paksa |
Getaran paksa adalah suatu getaran yang terjadi akibat adanya rangsangan dari gaya luar, apabila rangsangan ini berosilasi maka sistem tersebut akan dipaksa bergetar pada frekuensi rangsangannya. Apabila frekuensi rangsangannya sama dengan salah satu dari frekuensi natural sistem, maka akan diperoleh suatu keadaan resonansi dan osilasi besar yang cukup berbahaya dan mungkin mengakibatkan kerusakan pada beberapa objek struktur besar seperti gedung ataupun jembatan dan beberapa kejadian yang merupakan kejadian menakutkan yang dapat disebabkan oleh resonansi. Oleh karena itu perhitungan frekuensi natural merupakan hal yang penting dalam anilisis getaran atau vibrasi.

Post a Comment for "Pengertian dan Jenis Getaran Mekanik"